CALL US : 1-501-492-4300
Click on the grade level buttons above to take you to a master list of grade-level resources.
Note that a few buttons on each page are not yet active. We are working as fast as we can!
Algebra I



Click for...
TEACHER PLANNER Version 2.0
MODULE RESOURCES BOX Files
PINTEREST BOARD
Module 1:
Relationships Between Quantities and Reasoning with Equations and their Graphs
40-ish days
N-Q.1, N-Q.2, N-Q.3, A-SSE.1, A-SSE.2, A-APR.1, A-CED.1, A-CED.2, A-CED.3, A-CED.4, A-REI.1, A-REI.3, A-REI.5, A-REI.6, A-REI.10, A-REI.12
By the end of eighth grade, students have learned to solve linear equations in one variable and have applied graphical and algebraic methods to analyze and solve systems of linear equations in two variables. Now, students analyze and explain precisely the process of solving an equation. Students, through reasoning, develop fluency writing, interpreting, and translating between various forms of linear equations and inequalities and make conjectures about the form that a linear equation might take in a solution to a problem. They reason abstractly and quantitatively by choosing and interpreting units in the context of creating equations in two variables to represent relationships between quantities. They master the solution of linear equations and apply related solution techniques and the properties of exponents to the creation and solution of simple exponential equations. They learn the terminology specific to polynomials and understand that polynomials form a system analogous to the integers.
Click for...
MODULE RESOURCES
PINTEREST BOARD
Module 2:
Descriptive Statistics
25-ish days
S-ID.1, S-ID.2, S-ID.3, S-ID.5, S-ID.6, S-ID.7, S-ID.8, S-ID.9
This module builds upon students’ prior experiences with data, providing students with
more formal means of assessing how a model fits data. Students display and interpret graphical representations of data, and if appropriate, choose regression techniques when building a model that approximates a linear relationship between quantities. They analyze their knowledge of the contextof a situation to justify their choice of a linear model. With linear models, they plot and analyze residuals to informally assess the goodness of fit.
Click for...
TEACHER PLANNER under construction
MODULE RESOURCES
PINTEREST BOARD
Module 3:
Linear and Exponential Functions
35-ish days
A-SSE.3, A-CED.1, A-REI.11, F-IF.1, F-IF.2, F-IF.3, F-IF.4, F-IF.5, F-IF.6, F-IF.7, F-IF.9, F-BF.1, F-BF.3, F-LE.1, F-LE.2, F-LE.3, F-LE.5
In earlier grades, students defined, evaluated, and compared functions in modeling relationships between quantities. In this module, students learn function notation and develop the concepts of domain and range. They explore many examples of functions, including sequences; they interpret functions given graphically, numerically, symbolically, and verbally, translate between representations, and understand the limitations of various representations. Students build on their understanding of integer exponents to consider exponential functions with integer domains. They compare and contrast linear and exponential functions, looking for structure in each and distinguishing between additive and multiplicative change. Students explore systems of equations and inequalities, and they find and interpret their solutions. They interpret arithmetic sequences as linear functions and geometric sequences as exponential functions. In building models of relationships between two quantities, students analyze the key features of a graph or table of a function.

Click for...
TEACHER PLANNER under construction
MODULE RESOURCES
PINTEREST BOARD
Module 4:
Polynomial and Quadratic Expressions, Equations and Functions
30-ish days
N-RN.3, A-SSE.1, A-SSE.2, A.SSE.3, A-APR.1, A-APR.3, A-CED.1, A-CED.2, A-CED.4, A-REI.11, F-IF.4, F-IF.5, F-IF.6, F-IF.7, F-IF.8, F-IF.9, F-BF.3
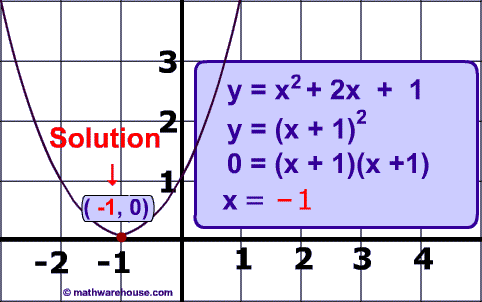
In this module, students build on their knowledge from Module 3. Students strengthen their ability to discern structure in polynomial expressions. They create and solve equations involving quadratic and cubic expressions. In this module’s modeling applications, students reason abstractly and quantitatively in interpreting parts of an expression that represent a quantity in terms of its context; they also learn to make sense of problems and persevere in solving them by choosing or producing equivalent forms of an expression (e.g., completing the square in a quadratic expression to reveal a maximum value). Students consider quadratic functions, comparing the key characteristics of quadratic functions to those of linear and exponential functions. They learn through repeated reasoning to anticipate the graph of a quadratic function by interpreting the structure of various forms of quadratic expressions. In particular, they identify the real solutions of a quadratic equation as the zeros of a related quadratic
function.
Click for...
TEACHER PLANNER
MODULE RESOURCES
PINTEREST BOARD
Module 5:
A Synthesis of Modeling with Equations and Functions
20-ish days
N-Q.3, A-CED.1, A-CED.2, F-IF.4, F-IF.5, F-IF.6, F-BF.1, F-LE.1, F-LE.2
In this module, students expand their experience with functions to include more specialized functions—linear, exponential, quadratic, square, and cube root, and those that are piecewise-defined, including absolute value and step. Students select from among these functions to model phenomena using the modeling cycle.
